I Radar ad Onda Continua (CW)
Principi di funzionamento dei radar CW.
Al contrario dei radar ad impulsi, quelli ad onda continua (CW) emettono radiazioni elettromagnetiche in maniera non discontinua nel tempo.
I normali radar CW non possono rilevare la distanza perché non vi è alcun ritardo tra l’ istante di emissione del segnale e il suo ritorno.
Sapendo che, nei radar ad impulsi, la distanza del bersaglio varia in funzione della durata di tempo tra l’ istante di trasmissione e quello di ricezione (ritardo), nei radar CW non verificandosi alcuna interruzione del segnale, non è possibile rilevare la distanza radiale rispetto al ricevitore, se non tramite l’ ausilio di altri sistemi che legano la distanza alla variazione di frequenza (modulatori di frequenza).
“Per quanto riguarda i radar a impulsi, l’ eco giunge al ricevitore con un ritardo R rispetto all’ istante d’ emissione, pari al tempo impiegato a percorrere due volte (andata e ritorno) la distanza D tra il radar e il bersaglio alla velocità della luce c (c=3x10^8 m/s). Poiché R è legato a D dalla relazione:nR=2D/c
misurando con un apposito dispositivo (indicatore) l’ intervallo T si risale alla misura della distanza D.„
Un radar CW ha la possibilità di misurare la variazione istantanea della velocità radiale del bersaglio rispetto al suo ricevitore, e quindi il suo avvicinamento o allontanamento.
Questo avviene mediante la misurazione diretta della variazione Doppler (o Doppler shift) nel segnale di ritorno.
Il Doppler shift è una variazione della frequenza dell’ onda elettromagnetica causata dal movimento relativo tra trasmettitore (sorgente) e ricevitore.
La lunghezza d’ onda è data dal rapporto tra la velocità di propagazione dell’ onda nel mezzo e la frequenza ondulatoria emessa.
Essendo il valore della velocità di propagazione costante, se la frequenza aumenta la lunghezza d’ onda si riduce.
La variazione tra la frequenza emessa e quella ricevuta è dunque definita come Doppler shift.
“Un onda elettromagnetica è considerata una perturbazione fisica prodotta in una regione dello spazio, che si propagata con moto ondulatorio, a partire dal punto sorgente, attraverso di esso e successivamente produce un effetto in un’ altra regione.
Si distinguono onde elastiche nei solidi, onde superficiali nei liquidi, onde acustiche, onde luminose e onde elettromagnetiche.
Alle onde elettromagnetiche è sempre associata energia raggiante.
Un onda piana si diffonde con velocità v detta di propagazione, essa dipende dalle caratteristiche del mezzo in cui essa si propaga:v=1/sqrt(eμ)
Dove e è la costante dielettrica, e μ è la permeabilità magnetica del mezzo (per l’ aria =12,56x10^ˉ7 H/m).
Nel caso in cui il mezzo sia il vuoto, la velocità v coincide con quella della luce c.
La lunghezza d’ onda λ delle onde elettromagnetiche risulta dalla relazione:λ=v/ƒ
Dove ƒ è la frequenza d’ oscillazione.
Se durante la propagazione le onde elettromagnetiche incontrano un ostacolo, esercitano su esso una pressione, detta pressione di radiazione. Inoltre possono essere riflesse o assorbite dal corpo, sul quale trasferiscono la propria energia, generando calore e determinandone un aumento di temperatura.
Nei sistemi radar vengono impiegate generalmente le microonde (UHF) a frequenza ultra alta (decimetriche):ƒ = 300-3000 MHz;
λ= 1m-10cm.„

Fig.1. Variazione Doppler dal trasmittente in movimento.
Dove s sta per speed, c per la velocità di propagazione, f per la frequenza d’ oscillazione, λ e λ’ è il periodo o la lunghezza d’ onda.
Se il ricevitore si muove in senso opposto alla direzione della propagazione, ci sarà un aumento della frequenza ricevuta.
Se il velivolo trasmettitore/ricevitore e il suo bersaglio sono in moto l’ uno verso l’ altro, la frequenza percepita dal ricevitore è maggiore di quella emessa.
Il valore risultante della variazione dipenderà dalla velocità relativa tra il T/R e l’ obiettivo lungo una linea, nota come line-of-sight (LOS), che è la linea di unione tra i due oggetti (raggio).

Fig.2. Determinazione della velocità relativa lungo la linea di unione tra i due aerei (velocità radiale).
La variazione Doppler può essere calcolata conoscendo le velocità effettiva del T/R e dell’ obiettivo (quella diretta lungo il suo asse longitudinale), denominate rispettivamente s1 e s2, e gli angoli compresi tra la loro direzione e la linea di unione, denominati q1 e q2.
La somma delle due velocità lungo la linea di unione (velocità radiale) è data dalla somma delle singole:
s = s1 cosq1 + s2 cosq2
Tale valore può essere interpretato anche come la velocità istantanea con il quale i due aerei, percorrendo la LOS, tendono alla collisione.
Gli angoli rappresentano:
q1= il rilevamento relativo con l’ obiettivo (spesso indicato come RIPLO o rilevamento polare, ossia quello che utilizza le ore dell’ orologio per indicare la posizione del bersaglio).
Oppure, la differenza tra la prua (angolo compreso tra il Nord e la direzione dell’ asse longitudinale dell’ aereo) del T/R e il rilevamento vero dell’ obiettivo (angolo compreso tra la direzione del Nord e la direzione dell’ aereo che vogliamo indicare).
Tutto ciò segue una vecchia regola nautica:
“Se due navi in avvicinamento si mantengono su di un rilevamento relativo costante, sussiste il pericolo di collisione.”
“Rilevamento Relativo = Rilevamento Vero – Prua = da 0° a 359°Non fa differenza se gli angoli sono positivi o negativi, poiché cos(-α)=cos(α).
q2 = è l’ angolo dell’ obiettivo (rilevamento relativo tra la linea di unione e la direzione dell’ obiettivo).
Calcolato in modo analogo rispetto al rilevamento relativo, tranne che la rotta dell’ obiettivo è sostituita dalla prua e viene utilizzato il rilevamento reciproco anziché il suo rilevamento vero. Il rilevamento reciproco si ottiene:Rilevamento Reciproco = Rilevamento + 180°
(Se la Torre di controllo ci rileva a 60°, per dirigerci verso l’ aeroporto, dovremo mettere in prua il reciproco, ossia 60+180=240°).
Non è necessario che questo risultato sia negativo, positivo o maggiore di 360° (anche se dovremmo utilizzare un campo da 0° a 359°).„
Presupposta la conoscenza del valore della velocità radiale Vp, la variazione della frequenza restituita (deviazione di frequenza) Df è:
Df = 2Vp/l
Dove l è la lunghezza d’ onda del segnale emesso.
Per esempio, la variazione Doppler in un radar ad onda continua con banda X (10 GHz) sarà di circa 30 Hz per ogni miglio orario di velocità radiale.
“L’ effetto Doppler si verifica tutte le volte che c’ è un moto relativo tra la sorgente di onde e l’ osservatore.
Per tale effetto l’ onda di eco ha una frequenza, diversa da quella di emissione, che diventa più alta se il bersaglio di avvicina, più bassa in caso contrario.
La deviazione di frequenza f è proporzionale alla velocità radiale Vp del bersaglio:Df = 2Vp/l
Questo radar permette quindi la misura della loro velocità radiale, ed è proprio questa la ragione per la quale i CW radar vengono impiegati.„
I sistemi di polizia utilizzano i radar CW per misurare la velocità (istantanea) degli autoveicoli.
I radar a onda continua vengono impiegati in applicazioni militari dove è necessaria la misurazione della velocità radiale dei bersagli.
Chiaramente, la velocità radiale può essere determinata anche con un sistema radar basato sugli impulsi tramite la misurazione della variazione della distanza da impulso a impulso.
RADAR CW A FREQUENZA MODULATA
(FMCW, Frequency Modulated Continuous Wave)
Come inizialmente accennato, è anche possibile utilizzare un radar CW per misurare la distanza, anziché la velocità, attraverso la modulazione di frequenza.
“La modulazione di frequenza si ha quando la frequenza d’ oscillazione sinusoidalea=Asen2π f0·t
viene fatta variare agendo sul valore di f0 in modo proporzionale al segnale da trasmettere.„
Il tempo di ritardo fra la trasmissione e la ricezione può essere determinato misurando le frequenze del segnale di ritorno; la distanza è quindi determinabile come precedentemente descritto.
La via più semplice per modulare l’ onda è di aumentarne linearmente la frequenza.
In altre parole, la frequenza emessa “varierà in maniera costante”.

Fig.3. Teoria del funzionamento della modulazione di frequenza di onde continua (FMCW).
I sistemi FMCW misurano la variazione istantanea fra la frequenza emesse e ricevuta, Df.
Questa variazione è direttamente proporzionale all’ intervallo di tempo, Dt, nel quale il segnale radar colpisce l’ obiettivo e poi ritorna (ritardo).
La distanza è ricavabile dalla formula
D = cDt/2
dove il ritardo e dato dalla seguente relazione:
Dt = T Df/(f2-f1)
dove:
f2= frequenza massima
f1 = frequenza minima
T = periodo della durata da f1 a f2,
Df = variazione tra la frequenza emessa e ricevuta.
Il sistema utilizza un dispositivo (disciminator) che lascia passare esclusivamente la parte positiva del segnale, che è direttamente proporzionale alla distanza (altrimenti i Df negativi daranno distanze negative, e ciò sarebbe impossibile ).
Questo è lo schema del sistema:
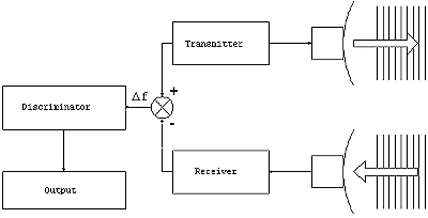
Fig.4. Schema a blocchi della FMCW.
Sostituendo, si ottiene la seguente formula:
D = cTDf/2(f2 - f1)
dove Df è la variazione tra la frequenza emessa e ricevuta.
Leggendo la formula si può notare che se il valore della frequenza di ritorno tende a quello di emissione (Df diminuisce), la distanza sta aumentando.
Un’ altra via per costruire un sistema FMCW , è confrontare le differenti fasi fra i segnali trasmessi e ricevuti dopo che le informazioni sulla durata sono state demodulate dal ricevitore.
Questo sistema non deve discriminare i valori negativi di Df.
In uno o nell’ altro caso tuttavia, la distanza massima effettiva sarà determinata in funzione del periodo, secondo la relazione:
effettiva = cT/2
I sistemi FMCW vengono spesso utilizzati per gli altimetri radar, o nei radar di ricerca dei missili.
Questi sistemi non hanno una distanza minima d’ impiego come quelli ad impulsi.
Comunque, questi non vengono utilizzati per il rilevamento a lunga distanza, perché la potenza necessario per la trasmissione sarebbe elevatissima.
Possiamo ricordare che potenza di picco e la potenza media in un sistema ad impulsi sono legate dal rapporto DC (duty cycle):
DC = Pmax / Pmedia
Per un sistema ad onda continua, il coefficiente vale uno: la potenza di picco è uguale a quella media.
Nei sistemi pulsanti ad impulsi la potenza di picco è nettamente superiore a quella media.
Dato che il radar a impulsi trasmette per periodi di tempo molto brevi implica il fatto che esse richiede una potenza molto elevata per tempi molto brevi, il rapporto di picco e potenza medio e per ciò molto elevato.
by Antonio "Blackviper" Rocca
2004